递归

你好，递归！

前面的章节中我们简要谈了一下递归。而在本章，我们会深入地了解到它为何在 Haskell 中是如此重要，能够以递归思想写出简洁优雅的代码。

如果你还不知道什么是递归，就读这个句子。哈哈！开个玩笑而已！递归实际上是定义函数以调用自身的方式。在数学定义中，递归随处可见，如斐波那契数列（fibonacci）。它先是定义两个非递归的数：F(0)=0,F(1)=1，表示斐波那契数列的前两个数为 0 和 1。然后就是对其他自然数，其斐波那契数就是它前面两个数字的和，即 F(N)=F(N-1)+F(N-2)。这样一来，F(3) 就是 F(2)+F(1)，进一步便是 (F(1)+F(0))+F(1)。已经下探到了前面定义的非递归斐波那契数，可以放心地说 F(3) 就是 2 了。在递归定义中声明的一两个非递归的值（如 F(0) 和 F(1)）也可以称作边界条件，这对递归函数的正确求值至关重要。要是前面没有定义 F(0) 和 F(1) 的话，它下探到 0 之后就会进一步到负数，你就永远都得不到结果了。一不留神它就算到了 F(-2000)=F(-2001)+F(-2002)，并且永远都算不到头！

递归在 Haskell 中非常重要。命令式语言要求你提供求解的步骤，Haskell 则倾向于让你提供问题的描述。这便是 Haskell 没有 while 或 for 循环的原因，递归是我们的替代方案。

实作 Maximum

maximum 函数取一组可排序的 List（属于 Ord Typeclass）做参数，并回传其中的最大值。想想，在命令式风格中这一函数该怎么实现。很可能你会设一个变量来存储当前的最大值，然后用循环遍历该 List，若存在比这个值更大的元素，则修改变量为这一元素的值。到最后，变量的值就是运算结果。唔！描述如此简单的算法还颇费了点口舌呢！

现在看看递归的思路是如何：我们先定下一个边界条件，即处理单个元素的 List 时，回传该元素。如果该 List 的头部大于尾部的最大值，我们就可以假定较长的 List 的最大值就是它的头部。而尾部若存在比它更大的元素，它就是尾部的最大值。就这么简单！现在，我们在 Haskell 中实现它

maximum' :: (Ord a) => [a] -> a  
maximum' [] = error "maximum of empty list"  
maximum' [x] = x  
maximum' (x:xs)   
    | x > maxTail = x  
    | otherwise = maxTail  
    where maxTail = maximum' xs

如你所见，模式匹配与递归简直就是天造地设！大多数命令式语言中都没有模式匹配，于是你就得造一堆 if-else 来测试边界条件。而在这里，我们仅需要使用模式将其表示出来。第一个模式说，如果该 List 为空，崩溃！就该这样，一个空 List 的最大值能是啥？我不知道。第二个模式也表示一个边缘条件，它说，如果这个 List 仅包含单个元素，就回传该元素的值。

现在是第三个模式，执行动作的地方。通过模式匹配，可以取得一个 List 的头部和尾部。这在使用递归处理 List 时是十分常见的。出于习惯，我们用个 where 语句来表示 maxTail 作为该 List 中尾部的最大值，然后检查头部是否大于尾部的最大值。若是，回传头部；若非，回传尾部的最大值。

我们取个 List [2,5,1] 做例子来看看它的工作原理。当调用 maximum' 处理它时，前两个模式不会被匹配，而第三个模式匹配了它并将其分为 2 与 [5,1]。 where 子句再取 [5,1] 的最大值。于是再次与第三个模式匹配，并将 [5,1] 分割为 5 和 [1]。继续，where 子句取 [1] 的最大值，这时终于到了边缘条件！回传 1。进一步，将 5 与 [1] 中的最大值做比较，易得 5，现在我们就得到了 [5,1] 的最大值。再进一步，将 2 与 [5,1] 中的最大值相比较，可得 5 更大，最终得 5。

改用 max 函数会使代码更加清晰。如果你还记得，max 函数取两个值做参数并回传其中较大的值。如下便是用 max 函数重写的 maximun'

maximum' :: (Ord a) => [a] -> a  
maximum' [] = error "maximum of empty list"  
maximum' [x] = x  
maximum' (x:xs) = max x (maximum' xs)

太漂亮了！一个 List 的最大值就是它的首个元素与它尾部中最大值相比较所得的结果，简明扼要。

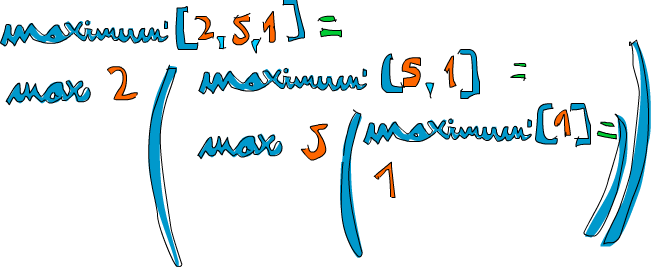
来看几个递归函数

现在我们已经了解了递归的思路,接下来就使用递归来实现几个函数. 先实现下 replicate 函数, 它取一个 Int 值和一个元素做参数, 回传一个包含多个重复元素的 List, 如 replicate 3 5 回传 [5,5,5]. 考虑一下, 我觉得它的边界条件应该是负数. 如果要 replicate 重复某元素零次, 那就是空 List. 负数也是同样, 不靠谱.

replicate' :: (Num i, Ord i) => i -> a -> [a]  
replicate' n x  
    | n <= 0    = []  
    | otherwise = x:replicate' (n-1) x

在这里我们使用了 guard 而非模式匹配, 是因为这里做的是布林判断. 如果 n 小于 0 就回传一个空 List, 否则, 回传以 x 作首个元素并后接重复 n-1 次 x 的 List. 最后, (n-1) 的那部分就会令函数抵达边缘条件.

*Note*: Num 不是 Ord 的子集, 表示数字不一定得拘泥于排序, 这就是在做加减法比较时要将 Num 与 Ord 型别约束区别开来的原因.

接下来实现 take 函数, 它可以从一个 List 取出一定数量的元素. 如 take 3 [5,4,3,2,1], 得 [5,4,3]. 若要取零或负数个的话就会得到一个空 List. 同样, 若是从一个空 List中取值, 它会得到一个空 List. 注意, 这儿有两个边界条件, 写出来:

take' :: (Num i, Ord i) => i -> [a] -> [a]  
take' n _  
    | n <= 0   = []  
take' _ []     = []  
take' n (x:xs) = x : take' (n-1) xs

首个模式辨认若为 0 或负数, 回传空 List. 同时注意这里用了一个 guard 却没有指定 otherwise 部分, 这就表示 n 若大于 0, 会转入下一模式. 第二个模式指明了若试图从一个空 List 中取值, 则回传空 List. 第三个模式将 List 分割为头部和尾部, 然后表明从一个 List 中取多个元素等同于令 x 作头部后接从尾部取 n-1 个元素所得的 List. 假如我们要从 [4,3,2,1] 中取 3 个元素, 试着从纸上写出它的推导过程

reverse 函数简单地反转一个 List, 动脑筋想一下它的边界条件! 该怎样呢? 想想...是空 List! 空 List 的反转结果还是它自己. Okay, 接下来该怎么办? 好的, 你猜的出来. 若将一个 List 分割为头部与尾部, 那它反转的结果就是反转后的尾部与头部相连所得的 List.

reverse' :: [a] -> [a]  
reverse' [] = []  
reverse' (x:xs) = reverse' xs ++ [x]

继续下去!

Haskell 支持无限 List，所以我们的递归就不必添加边界条件。这样一来，它可以对某值计算个没完, 也可以产生一个无限的数据结构，如无限 List。而无限 List 的好处就在于我们可以在任意位置将它断开.

repeat 函数取一个元素作参数, 回传一个仅包含该元素的无限 List. 它的递归实现简单的很, 看:

repeat' :: a -> [a]  
repeat' x = x:repeat' x

调用 repeat 3 会得到一个以 3 为头部并无限数量的 3 为尾部的 List, 可以说 repeat 3 运行起来就是 3:repeat 3 , 然后 3:3:3:3 等等. 若执行 repeat 3, 那它的运算永远都不会停止。而 take 5 (repeat 3) 就可以得到 5 个 3, 与 replicate 5 3 差不多.

zip 取两个 List 作参数并将其捆在一起。zip [1,2,3] [2,3] 回传 [(1,2),(2,3)], 它会把较长的 List 从中间断开, 以匹配较短的 List. 用 zip 处理一个 List 与空 List 又会怎样? 嗯, 会得一个空 List, 这便是我们的限制条件, 由于 zip 取两个参数, 所以要有两个边缘条件

zip' :: [a] -> [b] -> [(a,b)]  
zip' _ [] = []  
zip' [] _ = []  
zip' (x:xs) (y:ys) = (x,y):zip' xs ys

前两个模式表示两个 List 中若存在空 List, 则回传空 List. 第三个模式表示将两个 List 捆绑的行为, 即将其头部配对并后跟捆绑的尾部. 用 zip 处理 [1,2,3] 与 ['a','b'] 的话, 就会在 [3] 与 [] 时触及边界条件, 得到 (1,'a'):(2,'b'):[] 的结果,与 [(1,'a'),(2,'b')] 等价.

再实现一个标准库函数 -- elem! 它取一个元素与一个 List 作参数, 并检测该元素是否包含于此 List. 而边缘条件就与大多数情况相同, 空 List. 大家都知道空 List 中不包含任何元素, 便不必再做任何判断

elem' :: (Eq a) => a -> [a] -> Bool  
elem' a [] = False  
elem' a (x:xs)  
    | a == x    = True  
    | otherwise = a `elem'` xs

这很简单明了。若头部不是该元素, 就检测尾部, 若为空 List 就回传 False.

"快速"排序

假定我们有一个可排序的 List, 其中元素的型别为 Ord Typeclass 的成员. 现在我们要给它排序! 有个排序算法非常的酷, 就是快速排序 (quick sort), 睿智的排序方法. 尽管它在命令式语言中也不过 10 行, 但在 Haskell 下边要更短, 更漂亮, 俨然已经成了 Haskell 的招牌了. 嗯, 我们在这里也实现一下. 或许会显得很俗气, 因为每个人都用它来展示 Haskell 究竟有多优雅!

它的型别声明应为 quicksort :: (Ord a) => [a] -> [a], 没啥奇怪的. 边界条件呢? 如料，空 List。排过序的空 List 还是空 List。接下来便是算法的定义：排过序的 List 就是令所有小于等于头部的元素在先(它们已经排过了序), 后跟大于头部的元素(它们同样已经拍过了序)。注意定义中有两次排序，所以就得递归两次！同时也需要注意算法定义的动词为"是"什么而非"做"这个, "做"那个, 再"做"那个...这便是函数式编程之美！如何才能从 List 中取得比头部小的那些元素呢？List Comprehension。好，动手写出这个函数！

quicksort :: (Ord a) => [a] -> [a]  
quicksort [] = []  
quicksort (x:xs) =  
  let smallerSorted = quicksort [a | a <- xs, a <= x] 
      biggerSorted = quicksort [a | a <- xs, a > x]  
  in smallerSorted ++ [x] ++ biggerSorted

小小的测试一下, 看看结果是否正确~

ghci> quicksort [10,2,5,3,1,6,7,4,2,3,4,8,9]  
[1,2,2,3,3,4,4,5,6,7,8,9,10]  
ghci> quicksort "the quick brown fox jumps over the lazy dog"  
" abcdeeefghhijklmnoooopqrrsttuuvwxyz"

booyah! 如我所说的一样! 若给 [5,1,9,4,6,7,3] 排序，这个算法就会取出它的头部，即 5。将其置于分别比它大和比它小的两个 List 中间，得 [1,4,3] ++ [5] ++ [9,6,7], 我们便知道了当排序结束之时，5会在第四位，因为有3个数比它小每，也有三个数比它大。好的，接着排 [1,4,3] 与 [9,6,7], 结果就出来了！对它们的排序也是使用同样的函数，将它们分成许多小块，最终到达临界条件，即空 List 经排序依然为空，有个插图：

橙色的部分表示已定位并不再移动的元素。从左到右看，便是一个排过序的 List。在这里我们将所有元素与 head 作比较，而实际上就快速排序算法而言，选择任意元素都是可以的。被选择的元素就被称作锚（pivot），以方便模式匹配。小于锚的元素都在浅绿的部分，大于锚都在深绿部分，这个黄黄的坡就表示了快速排序的执行方式：

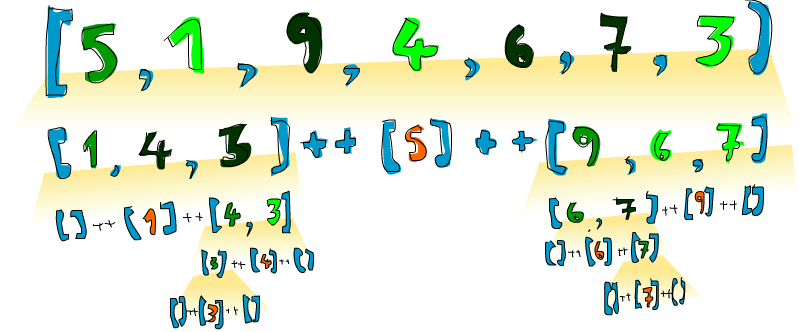
用递归来思考

我们已经写了不少递归了，也许你已经发觉了其中的固定模式：先定义一个边界条件，再定义个函数，让它从一堆元素中取一个并做点事情后，把余下的元素重新交给这个函数。这一模式对 List、Tree 等数据结构都是适用的。例如，sum 函数就是一个 List 头部与其尾部的 sum 的和。一个 List 的积便是该 List 的头与其尾部的积相乘的积，一个 List 的长度就是 1 与其尾部长度的和. 等等

再者就是边界条件。一般而言，边界条件就是为避免进程出错而设置的保护措施，处理 List 时的边界条件大部分都是空 List，而处理 Tree 时的边界条件就是没有子元素的节点。

处理数字时也与之相似。函数一般都得接受一个值并修改它。早些时候我们编写过一个计算 Factorial 的函数，它便是某数与它减一的 Factorial 数的积。让它乘以零就不行了， Factorial 数又都是非负数，边界条件便可以定为 1，即乘法的单比特。因为任何数乘以 1 的结果还是这个数。而在 sum 中，加法的单比特就是 0。在快速排序中，边界条件和单比特都是空 List，因为任一 List 与空 List 相加的结果依然是原 List。

使用递归来解决问题时应当先考虑递归会在什么样的条件下不可用, 然后再找出它的边界条件和单比特, 考虑参数应该在何时切开(如对 List 使用模式匹配), 以及在何处执行递归.